This article was updated on December 2, 2021. The three separate blog articles on calibration uncertainty were combined into this one article. Also, some other updates were made.
If you don’t know the measurement uncertainty, don’t make the measurement at all!
This time we are talking about a very fundamental consideration in any measurement or calibration – uncertainty !
I made a white paper on the basics of uncertainty in measurement and calibration. It is designed for people who are responsible for planning and performing practical measurements and calibrations in industrial applications but who are not mathematicians or metrology experts.
You can download the free white paper as a pdf file by clicking the below picture:
Table of content
- Intro
- What is measurement uncertainty?
- Classic “piece of string” uncertainty example
- Uncertainty components
- Your reference standard (calibrator) and its traceability
- Other sources of uncertainty
- Is it passed or failed calibration?
- Examples
- TUR / TAR ratio vs. uncertainty calculation
- Summary & the key takeaways
It seems that the generic awareness of and interest in uncertainty is growing, which is great.
The uncertainty of measurements can come from various sources such including the reference measurement device used to perform the measurement, the environmental conditions, the person performing the measurements, the procedure, and other sources.
There are several calibration uncertainty guides, standards, and resources available out there, but these are mostly just full of mathematical formulas. In this paper, I have tried to keep the mathematic formulas to a minimum.
Uncertainty estimation and calculation can be pretty complicated, but I have tried my best to make some sense out of it.
What is measurement uncertainty?
What is the uncertainty of measurement? Put simply, it is the “doubt” in the measurement, so it tells us how good the measurement is. Every measurement we make has some “doubt” and we should know how much in order to be able to decide if the measurement is good enough to be used.
It is good to remember that error is not the same as uncertainty. In calibration, when we compare our device to be calibrated against the reference standard, the error is the difference between these two readings. The error is meaningless unless we know the uncertainty of the measurement.
Classic “piece of string” uncertainty example
Let’s take a simple example to illustrate the measurement uncertainty in practice; we give the same piece of a string to three different people (one at a time) and ask them to measure the length of that string. There are no additional instructions given. They can use their own tools and methods to measure it.
More than likely, you will get three somewhat different answers. For example:
- The first person says the string is about 60 cm long. He used a 10 cm plastic ruler and measured the string once and came to this conclusion.
- The second person says it is 70 cm long. He used a three-meter measuring tape and checked the results a couple of times to make sure he was right.
- The third person says it is 67.5 cm long with an uncertainty of ±0.5 cm. He used an accurate measuring tape and measured the string several times to get an average and standard deviation. Then, he tested how much the string stretches when it was pulled and noticed that this had a small effect on the result.
Even this simple example shows that there are many things that affect the result of measurement: the measurement tools that were used, the method/process that was used, and the way that the person did the job.
So, the question you should be asking yourself is:
At your plant, when calibration work is performed, which of these three above examples will it be?
What kind of “rulers” are being used at your site and what are the measuring methods/processes?
If you just measure something without knowing the related uncertainty, the result is not worth much.
Uncertainty components
Standard deviation – an important component of uncertainty
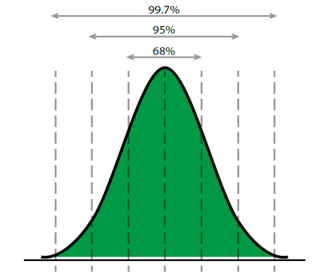
Several components make up total measurement uncertainty, and one of the most important is standard deviation, so let’s discuss that next.
A simple, yet worthwhile practice is to repeat a measurement/calibration several times instead of just performing it once. You will most likely discover small differences in the measurements between repetitions. But which measurement is correct?
Without diving too deep into statistics, we can say that it is not enough to measure once. If you repeat the same measurement several times, you can find the average and the standard deviation of the measurement and learn how much the result can differ between repetitions. This means that you can find out the normal difference between measurements.
You should perform a measurement multiple times, even up to ten times, for it to be statistically reliable enough to calculate the standard deviation.
These kinds of uncertainty components, which you get by calculating the standard deviation, are called A-type uncertainty components.
But repeating the same measurement ten times is just not possible in practice, you may say.
Luckily you don’t always need to perform ten repetitions, but you should still experiment with your measurement process by sometimes repeating the same measurement several times. This will tell you what the typical deviation of your whole measurement process is, and you can use this knowledge in the future as an uncertainty component related to that measurement, even if you only perform the measurement once during your normal calibration.
Imagine that when performing a temperature measurement/calibration multiple times, you learn that there is a ±0.2 °C difference between the repetitions. Next time you perform the same measurement – even if you only perform it once – you would be aware of this possible ±0.2 °C difference, so you could take it into account and not let the measurement get too close to the acceptance limit.
If you calibrate similar kinds of instruments repeatedly, it is often enough to perform the measurement just once and use the typical experimental standard deviation.
In summary, you should always be aware of the standard deviation of your calibration process – it is an important part of the total uncertainty.
Your reference standard (calibrator) and its traceability
One of the biggest sources of uncertainty often comes from the reference standard (or calibrator) that you are using in your measurements / calibrations.
Naturally, to start with you should select a suitable reference standard for each measurement.
It is also important to remember that it is not enough to use the manufacturer’s accuracy specification for the reference standard and keep using that as the uncertainty of the reference standards for years.
Instead, you must have your reference standards calibrated regularly in a calibration laboratory that has sufficient capabilities (a small enough uncertainty) to calibrate the standard and to make it traceable. Pay attention to the total uncertainty of the calibration that the laboratory documents for your reference standard.
Also, you should follow the stability of your reference standard between calibrations. After some time, you will learn the true uncertainty of your reference standard and you can use that information in your calibrations.
Other sources of uncertainty
In the white paper you can find more detailed discussion on the other sources of uncertainty.
These include:
- Device under test (DUT)
- Reference standard (calibrator)
- Method/process for performing the measurements/calibrations
- Environmental conditions
- The person(s) performing the measurements
- Additional uncertainty components depending on the quantity being measured/calibrated
These uncertainty components are referred to as type B uncertainty components.
Is it passed or failed calibration?
In this section we discuss the following scenario: You have performed the calibration, you have the results on a certificate, and you have compared the results to the tolerance limits. It’s time to pop the big questions: Is it a passed or failed calibration? Is it in or out of tolerance?
Compliance statement – pass or fail
Typically, when you calibrate an instrument you have predefined tolerance limits that the instrument has to meet. Sure, you may perform some calibrations without tolerance limits, but in process industries the tolerance levels are typically set in advance.
Tolerance levels indicate how much the result can differ from the true value. If the errors of the calibration result are within the tolerance limits, it is a passed calibration, and if some of the errors are outside of tolerance limits, it is a failed calibration. This sounds simple, like basic mathematics. How hard can it be?
It is important to remember that it is not enough to just take the error into account; you must also take the total uncertainty of the calibration into account!
Taking the uncertainty into account turns this into a whole different ball game. As discussed in the white paper, there are many sources of uncertainty. Let’s go through some examples next.
Example #1 - reference with too big uncertainty
Let’s say the process transmitter you are about to calibrate has a tolerance level of ±0.5% of its measurement range.
During the calibration you find out that the biggest error is 0.4%, so this sounds like a pass calibration, right?
But what if the calibrator that was used has an uncertainty specification of ±0.2%? Then the 0.4% result could be either a pass or a fail – it is impossible to know which.
Plus, in any calibration you also have uncertainty caused by many other sources, like the standard deviation of the result, repeatability, the calibration process, environmental conditions, etc.
When you estimate the effect of all these uncertainty components, it is even more likely that the calibration was a fail after all, even though it looked like a pass at first.
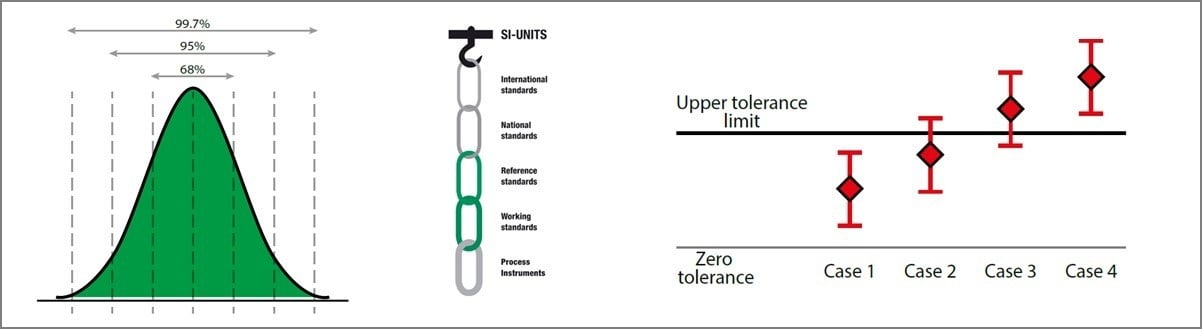
Example #2 - different cases
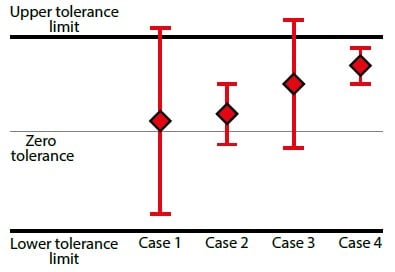
Let’s look at a graphical illustration of the next example to make this easier to understand. In the picture below there are four calibration points taken, the diamond shape indicating the actual calibration result. The line above and below the result indicates the total uncertainty for each calibration point. The black horizontal line marks the tolerance limit.
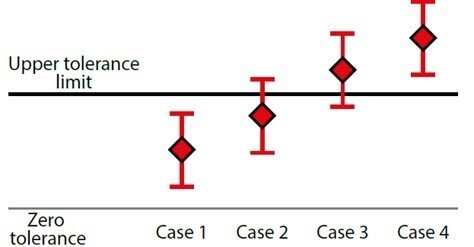
We can interpret the different cases shown above as follows:
- Case 1: This is clearly within the tolerance limits, even when uncertainty is taken into account. So we can state this as a pass.
- Case 4: This is also a clear case. The result is outside of the tolerance limits, even before uncertainty is taken into account, so this is clearly a fail.
- Cases 2 and 3: These are a bit more difficult to judge. It seems that in case 2 the result is within the tolerance limit while in case 3 it is outside, especially if you don’t care about the uncertainty. But taking the uncertainty into account, we can’t really say this with confidence.
There are regulations (for example, ILAC G8:1996 – Guidelines on Assessment and Reporting of Compliance with Specification; EURACHEM / CITAC Guide: Use of uncertainty information in compliance assessment, First Edition 2007) for how to state the compliance of a calibration.
These guides suggest that a result should only be considered a pass when the error plus the uncertainty is less than the tolerance limit.
They also suggest that a result should only be considered a fail when the error with the uncertainty added or subtracted is greater than the tolerance limit.
When the result is closer to the tolerance limit than half of the uncertainty, they suggest it should be called an “undefined” situation, i.e. you should not state the result as a pass or fail.
We have seen many people interpreting the uncertainty and pass/fail decision in many different ways over the years. In practice, uncertainty is often not taken into account in the pass/fail decision-making process, but it is nonetheless very important to be aware of the uncertainty when making a decision.
Example #3 – different uncertainties
Another situation to illustrate is when the total uncertainty is not always the same.
Cases 1 and 2 have about the same measurement result , so without uncertainty we would consider these as the same level measurements.
But when the uncertainty is taken into account, we can see that case 1 is really terrible because the uncertainty is simply too large to be used for this measurement with the given tolerance limits.
Looking at cases 3 and 4 it seems that case 3 is better, but with uncertainty we can see that it is not good enough for a pass statement, while case 4 is.
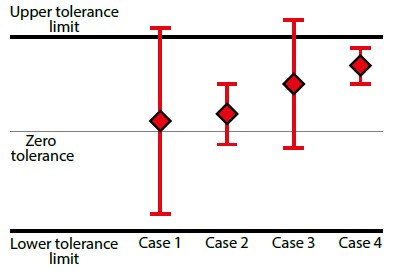
Again, I want to point out that we need to know the uncertainty before we can judge a measurement result. Without the uncertainty calculation, cases 1 and 2 look similar; with uncertainty taken into account they are very different.
TUR / TAR ratio vs. uncertainty calculation
TUR (test uncertainty ratio) and TAR (test accuracy ratio) are often mentioned in various publications. Some publications even suggest that with a large enough TUR/TAR ratio there is no need to worry about uncertainty estimation / calculation.
A commonly used TAR ratio is 4:1. In short this means that if you want to calibrate a 1% instrument, your test equipment should be four times more accurate, i.e., it should have an accuracy of 0.25% or better.
Some guides/publications also have recommendations for the ratio. Most often the ratio is used as in the above example, i.e., to compare the specifications of the device under test (DUT) and the manufacturer’s specifications of the reference standard.
But in that scenario you only consider the reference standard (test equipment, calibrator) specifications and you neglect all other related uncertainties.
While this may be “good enough” for some calibrations, this system does not take all uncertainty sources into account.
For an accurate result it is highly recommended that you perform the uncertainty evaluation/calculation, taking into account the whole calibration process.
A question we are asked regularly is “How many times more accurate should the calibrator be compared to the device to be calibrated?”. While some suggestions could be given, there isn’t really any correct answer to this question. Instead, you should be aware of the total uncertainty of your calibrations. And of course, it should reflect your needs!
Summary & the key takeaways from the white paper
To learn more about this subject, please download and read the white paper linked in this post.
Here is a short list of the key takeaways:
- Be sure to distinguish between “error” and “uncertainty”.
- Experiment by performing multiple repetitions of measurements to gain knowledge of the typical deviation.
- Use appropriate reference standards (calibrators) and make sure they have a valid traceability to national standards and that the uncertainty of the calibration is known and suitable for your applications.
- Consider if the environmental conditions have a significant effect on the uncertainty of your measurements.
- Be aware of the readability and display resolution of any indicating devices.
- Study the important factors of the specific quantities you are calibrating.
- Familiarize yourself with the “root sum of the squares” method to add independent uncertainties together.
- Be aware of the coverage factor/confidence level/expanded uncertainty of the uncertainty components.
- Instead of or in addition to the TUR/TAR ratio, strive to be more aware of all the related uncertainties.
- Pay attention to the total uncertainty of the calibration process before making pass/fail decisions.
Download the free white paper article in pdf format by clicking the below image:
You may also like this one related to uncertainty:
Also, please check out the article What is calibration on our website.














.jpg)





.png)
.png)
Discussion