Dans ce post nous allons étudier le scénario suivant : Vous avez effectué un étalonnage, reporter les résultats sur un certificat et vous comparez ces résultats à votre tolérance. Il est temps de poser LA question : Est-ce que votre étalonnage est conforme ou non-conforme ? Autrement dit, est-ce que les résultats se trouvent dans mes tolérances ?
Ce post est le troisième et dernier post de notre série sur l’incertitude d’étalonnage. Si vous n’avez pas lu les deux premières parties de cet article, vous pouvez les trouver sur les pages précédentes du blog (ou en cliquant sur les liens ci-dessous). Si vous souhaitez lire toutes les parties, téléchargez le livre blanc associé à partir du lien ci-dessous.
Incertitude d'étalonnage pour les non mathématiciens - Partie 1
Incertitude d'étalonnage pour les non mathématiciens - Partie 2 : Les composantes d'incertitude
Jugement de conformité – Conforme ou Non-conforme
Bien souvent lorsque vous vérifiez un instrument, vous avez des limites de tolérances que l’instrument doit respecter. Evidemment, vous avez peut-être déjà effectuer des étalonnages sans limites de tolérances mais dans l’industrie de transformation des limites sont définies par avance et nous parlons donc de vérification. Les niveaux de tolérance sont les niveaux maximums indiquant dans quelle mesure le résultat peut différer de la valeur réelle. Si les erreurs du résultat de l'étalonnage se situent dans les limites de tolérance, il s'agit d'une vérification Conforme et si certaines des erreurs de résultat sont en dehors des limites de tolérance, il s'agit d'une vérification Non-conforme. Cela semble assez simple, comme les mathématiques de base. Mais jusqu’à quel point ?
Il est en tout cas important de se rappeler qu'il ne suffit pas de prendre en compte l'erreur, il faut également tenir compte de l'incertitude totale de l’étalonnage !
Prendre en compte l'incertitude redéfinit complétement les règles du jeu. Comme nous l’avons évoqué, il existe de nombreuses sources d’incertitude. Voyons quelques exemples…
Exemple
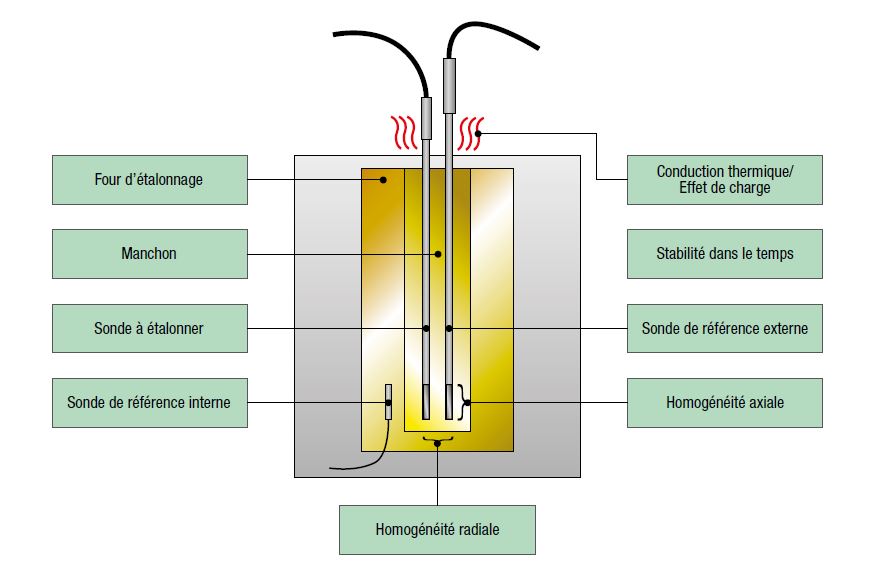
Supposons que le transmetteur que vous êtes sur le point d’étalonner possède une tolérance de ± 0,5% de sa plage de mesure. Lors de l’étalonnage, vous découvrez que l’erreur maximale est de 0,4%. Cela ressemble donc à un étalonnage conforme, n’est-ce pas? Mais qu'en est-il si le calibrateur utilisé a une incertitude de ± 0,2%? Une erreur de 0,4% pourrait ainsi signifier que l’étalonnage est conforme ou non-conforme, il est impossible de le savoir. De plus, lors de tout étalonnage, il existe de nombreuses autres sources d’incertitude telles que l’écart type du résultat, la répétabilité, le processus d’étalonnage, les conditions environnementales, etc. Lorsque vous estimez l'effet de toutes ces composantes d'incertitude, il est encore plus probable que dans cet exemple, l’étalonnage soit finalement non-conforme, même s'il semblait conforme a priori.
Exemple – Cas différents
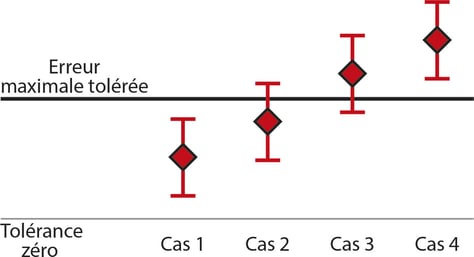
Examinons une illustration graphique du prochain exemple pour faciliter la compréhension. Dans l'image ci-dessous, quatre points d'étalonnage ont été réalisés, la forme en losange reflétant le résultat d'étalonnage réel. La ligne au-dessus et en-dessous du résultat indique l'incertitude totale pour cet étalonnage. Le niveau de tolérance est marqué par une ligne dans l'image.

Nous pouvons interpréter les différents cas présenter ci-dessous comme ceci :
- Cas 1: Ceci se trouve assez clairement dans les limites tolérées, même en tenant compte de l’incertitude. Nous pouvons donc appeler cela un bon résultat de « conformité ».
- Cas 4: Il s’agit là aussi d’un cas assez clair. Le résultat est en dehors des limites tolérées, même en tenant compte de l’incertitude. Nous pouvons donc appeler cela un mauvais résultat, ou une « non-conformité ».
- Cas 2 et Cas 3: Ces cas sont un peu plus difficiles à juger. Bien sûr, il semble que dans le cas 2, le résultat soit compris dans les limites tolérées tandis que dans le cas 3, il est en dehors, particulièrement si vous ne voulez pas tenir compte de l’incertitude. Mais si vous tenez compte de l’incertitude, vous ne pouvez pas vraiment l’affirmer avec certitude.
Il existe des réglementations (par exemple . ILAC G8:1996 - Directives sur l’évaluation et les rapports de conformité avec spécification ; Guide EURACHEM / CITAC : Usage des informations d’incertitude dans l’évaluation de la conformité, Première Édition 2007) sur la manière de déclarer la conformité de l’étalonnage. Ces guides suggèrent de déclarer un résultat comme étant conforme seulement quand l’erreur additionnée de l’incertitude est inférieure à la limite de conformité. Ils suggèrent également de ne déclarer comme non-conforme que les erreurs ajoutées (ou soustraites) de l’incertitude qui sont supérieures à la limite de conformité. Quand le résultat est plus proche de la limite de conformité que de la moitié de l’incertitude, il est suggéré de l’appeler « situation indéfinie », c’est-à-dire que vous ne devez déclarer ni conformité, ni nonconformité.
Nous avons vu de nombreuses personnes interpréter l’incertitude et les décisions de conformité/non-conformité de nombreuses façons différentes tout au long des années. En pratique, l’incertitude est plus souvent ignorée lors de la décision de conformité, mais il est de toute façon très important d’être conscient de l’incertitude, quand on prend la décision.
Exemples d’incertitude
Les graphiques ci-dessous montrent des exemples de ce que différentes incertitudes peuvent signifier en pratique. Les cas 1 et 2 ont le même résultat de mesure, et donc sans incertitude, on pourrait considérer ces deux cas comme identiques. Mais lorsqu’on tient compte de l’incertitude, on peut voir que le cas 1 est vraiment terrible puisque l’incertitude est simplement trop importante pour être utilisée pour cette mesure avec les limites de tolérance données.
Quand on regarde les cas 3 et 4, il semble que le cas 3 soit meilleur, mais avec l’incertitude, on voit qu’il n’est pas assez bon pour une déclaration de conformité, tandis que le cas 4 l’est.
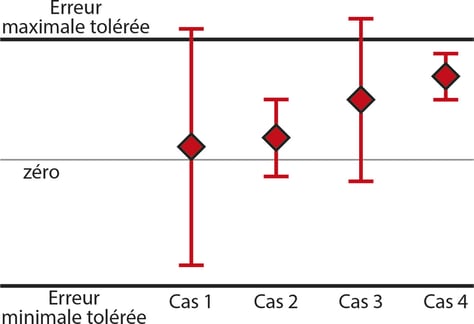
Je veux encore une fois souligner qu’il nous faut connaître l’incertitude avant de pouvoir juger le résultat d’une mesure. Sans le calcul de l’incertitude, les cas 1 et 2 ci-dessus semblent similaires, bien qu’en tenant compte de l’incertitude, ils sont très différents.
Comparaison de la capabilité (rapport TUR/TAR) et du calcul de l’incertitude
Le TUR (rapport d’incertitude du test), ou le TAR (rapport d’exactitude du test), est souvent mentionné dans diverses publications. En bref, cela signifie que si vous voulez étalonner un instrument ayant une exactitude d’1 % et vous voulez obtenir un rapport de 4:1, votre étalon doit être 4 fois plus précis, c’est-à-dire avoir une exactitude de 0,25 % ou meilleure. Certaines publications suggèrent que si la capabilité est suffisamment grande, il n’y a aucun besoin de se préoccuper de l’estimation/du calcul de l’incertitude. Le rapport utilisé le plus communément est 4:1. Certains guides/publications ont aussi des recommandations pour le rapport.
La plupart du temps, la capabilité est utilisée comme dans l’exemple ci-dessus, c’est-à-dire simplement pour comparer les spécifications du dispositif testé (DUT) et les spécifications du fabricant de l’étalon de référence. Mais dans ce scénario, on ne tient compte que des spécifications de l’étalon de référence (équipement de test, calibrateur) et on néglige toutes les autres incertitudes associées. Bien que ceci soit « suffisant » pour certains, les étalonnages effectués avec ce système ne tiennent pas compte de certaines des plus grandes sources d’incertitude. Il est donc fortement recommandé d’effectuer l’évaluation/le calcul de l’incertitude de l’ensemble du processus d’étalonnage.
On nous demande aussi assez régulièrement : « Combien de fois plus précis le calibrateur doit-il être par rapport au dispositif à étalonner ? » Bien que l’on pourrait donner certaines suggestions, il n’y a pas vraiment de réponse correcte à cette question. Au lieu de cela, il vous faut être conscient de l’incertitude totale de vos étalonnages. Et bien sûr, elle doit refléter vos besoins !
Résumé – points essentiels du livre blanc
Pour en apprendre plus sur le sujet, veuillez lire le livre blanc associé. Vous trouverez ci-dessous une liste des points essentiels à retenir de ce livre blanc:
- Assurez vous de faire la distinction entre “erreur” et “incertitude”
- Essayez en faisant plusieurs répétitions de mesures pour connaitre ce qu’est un écart
- Utilisez des références appropriées (calibrateurs) et s’assurer qu’ils disposent d’une traçabilité
aux standards nationaux et que l’incertitude de l’étalonnage est connue et adaptée à vos applications - Considérez que les conditions environnementales ont un effet significatif sur l’incertitude de vos mesures
- Soyez conscient de la lisibilité et de la résolution de tout indicateur
- Étudiez les facteurs importants spécifiques des grandeurs que vous calibrez
- Familiarisez-vous avec la “Méthode des moindres carrés” pour ajouter l’ensemble des incertitudes
- Soyez conscient du facteur de couverture / du niveau de confiance / Incertitude élargie, des composantes de l’incertitude
- Plutôt, ou en plus du ratio TUR / TAR, soyez conscient de toutes les incertitudes connexes
- Faites attention à l’incertitude totale du process d’étalonnage avant de prendre des décisions de conformité / non conformité
Bon étalonnage !
Original blog post: Calibration uncertainty for dummies - Part 3: Is it Pass or Fail?
Published: 4.1.2017
Written by: Heikki Laurila


























Discussion