Mätosäkerhet vid kalibrering för icke-matematiker

I denna blogg behandlar vi grunderna i mätosäkerhet vid mätning och kalibrering. Den är inte skriven för matematiker eller experter på metrologi, utan snarare för dig som planerar och utför praktiska mätningar och kalibreringar i industriella tillämpningar.

Att vara medveten om den mätosäkerhet som hänger ihop med mätning är mycket grundläggande, så om du inte är det, borde du egentligen inte göra några mätningar. Allmänt taget verkar det som att medvetenheten och intresset för mätosäkerhet växer, vilket är en bra sak. 

Mätosäkerhet kan härröra från olika källor, såsom från referensmätinstrumentet som används vid mätningen, miljöförhållanden, personen som gör mätningarna och från många andra källor. 

Det finns ett antal handböcker, standarder och resurser som behandlar mätosäkerhet vid kalibrering. För det mesta är de fyllda av matematiska formler, så i den här vitboken kommer jag att försöka hålla de matematiska formlerna till ett minimum. 

Det här är en praktisk handbok som kan ge lite allmän förståelse för den stora världen av mätosäkerhet inom mätning och kalibrering.

Klassiskt exempel med "ett snöre"

Låt oss börja med ett exempel för att illustrera mätosäkerheten i praktiken. I exemplet ger vi samma snöre till tre personer (en i taget) och ber dem mäta längden på snöret. Det är de enda instruktioner personerna får. Alla tre får använda sina egna verktyg och metoder för att mäta det. 

Det är högst troligt att det hela resulterar i att du får tre något olika svar, till exempel:

• Den första personen säger att snöret är cirka 60 cm långt. Hen använde en 10 cm lång plastlinjal, mätte snöret en gång och kom fram till denna slutsats.
• Den andra personen säger att det är 70 cm. Hen använde ett tre meter långt måttband och kontrollerade resultatet ett par gånger för att försäkra sig om att hen hade rätt.
• Den tredje personen säger att snöret är 67,5 cm, med en mätosäkerhet på ±0,5 cm. Hen använde ett exakt måttband och mätte snöret flera gånger för att få ett medeltal och en standardavvikelse. Dessutom testade hen hur mycket snöret töjer sig när det dras ut och märkte att detta hade en liten inverkan på resultatet.

Till och med detta förenklade exempel visar att det finns många saker som påverkar resultatet av en mätning, som exempelvis vilka mätverktyg som används, metoden/processen som används och hur personen utförde uppgiften. 

Så frågan du bör ställa dig själv är: 

När kalibreringsarbete utförs på din anläggning, vilket av dessa tre exempel tycker du låter mest bekant? 

Vilken typ av "linjaler" används på din arbetsplats och vilka är mätmetoderna/processerna? 

Om man mäter något bara en gång, utan att känna till den relaterade mätosäkerheten, är resultatet inte värt mycket.

Mycket kort lektion i terminologi

Låt oss ta en mycket kort titt på de grundläggande termerna som hänger samman med temat. 

Mätosäkerhet, vad är det egentligen? Vi kan helt enkelt säga att det är vårt "tvivel" på mätningen, vilket betyder att det talar om för oss hur bra vår mätning är. Varje mätning vi gör förknippas med ett visst mått av "tvivel" och vi bör veta hur starkt detta "tvivel" är för att kunna avgöra om mätningen är tillräckligt bra för ändamålet. 

Det är skäl att komma ihåg att ett fel inte är detsamma som mätosäkerhet. När vi jämför den enhet som ska kalibreras med referensnormalen är felet skillnaden mellan dessa två mätningar. Men felet har ingen betydelse om vi inte känner till mätosäkerheten i mätningen. 

Därför skulle jag vilja säga: 

Om du inte känner till mätosäkerheten i mätningen, låt bli att göra mätningen överhuvudtaget! 

Alltför ofta har vi sett exempel liknande detta: En person gör en viktig temperaturmätning i sin process med en toleransgräns på låt oss säga ±1,0 °C. Hen hittar ett maximalt fel på 0,5 °C, blir nöjd och säger att det är "godkänt” och accepterar resultatet. Även om hen, efter att ha analyserat kalibreringsprocessen, kunde se att den totala mätosäkerheten för mätprocessen är ±2,0 °C. Med andra ord var sättet som kalibreringen gjordes på inte tillräckligt bra för denna tillämpning. 

Men så länge hen inte kände till/brydde sig om mätosäkerheten kunde hen hävda att det var ett bra resultat och kalibreringen "godkänd", även om den i själva verket hade misslyckats.

Från att göra en enda mätning till att känna till din standardavvikelse

Vad ska du då göra för att starta resan mot att bli medveten om alla relaterade mätosäkerheter? 

Det första enkla, men goda, rådet är att om du vanligtvis gör en mätning/kalibrering en gång, försök i stället att upprepa samma mätning flera gånger. Högst sannolikt kommer du att upptäcka små skillnader mellan de upprepade mätningarna. Men vilken mätning är den korrekta? 

Utan att göra någon djupdykning i den statistiska vetenskapen, kan vi säga att det inte räcker med att bara mäta en gång. Om du upprepar samma mätning flera gånger, kan du hitta medelvärdet och standardavvikelsen för mätningen. Du kommer alltså att lära dig hur mycket resultaten kan skilja sig åt mellan upprepningarna. Du kan således ta reda på vad som är den normala skillnaden mellan mätningarna. 

Det rekommenderas att man upprepar en mätning många gånger, till och med upp till tio gånger, för att den statistiskt sett ska vara tillräckligt tillförlitlig för att beräkna standardavvikelsen. Den här typen av mätosäkerhetskomponenter, som man får genom att beräkna standardavvikelsen, kallas för mätosäkerhet av A-typ. 

Men då kanske du invänder: Vad menar du? – Det är helt enkelt inte möjligt i praktiken att alltid upprepa samma mätning tio gånger! 

Som tur är behöver du inte alltid upprepa mätningen tio gånger, men du bör ändå experimentera med din mätprocess genom att ibland göra flera repetitioner av samma mätning. På så sätt får du reda på vad den typiska avvikelsen för hela mätprocessen är. Sedan kan du använda denna kunskap framöver som en mätosäkerhetskomponent i samband med just den mätningen, även om du bara gör mätningen en gång under din normala kalibrering.

Föreställ dig att du utför en temperaturmätning/kalibrering flera gånger och du upptäcker att det kan vara en skillnad på ±0,2 °C mellan upprepningarna. Nästa gång du gör samma mätning, även om du då gör den bara en gång, skulle du vara medveten om att denna eventuella skillnad på ±0,2 °C finns. Då kan du ta hänsyn till det och inte låta mätningen gå alltför nära toleransgränsen.

Med andra ord om du kalibrerar liknande typer av instrument om och om igen, räcker det ofta med att göra bara en mätning och dra nytta av den typiska experimentella standardavvikelsen. Naturligtvis måste du göra hemläxan och utföra mätningarna och beräkningarna för att ta reda på den typiska standardavvikelsen för den aktuella instrumenttypen och kalibreringsprocessen.

Sammanfattningsvis bör du alltid vara medveten om standardavvikelsen för din kalibreringsprocess – den är en del av den totala mätosäkerheten.

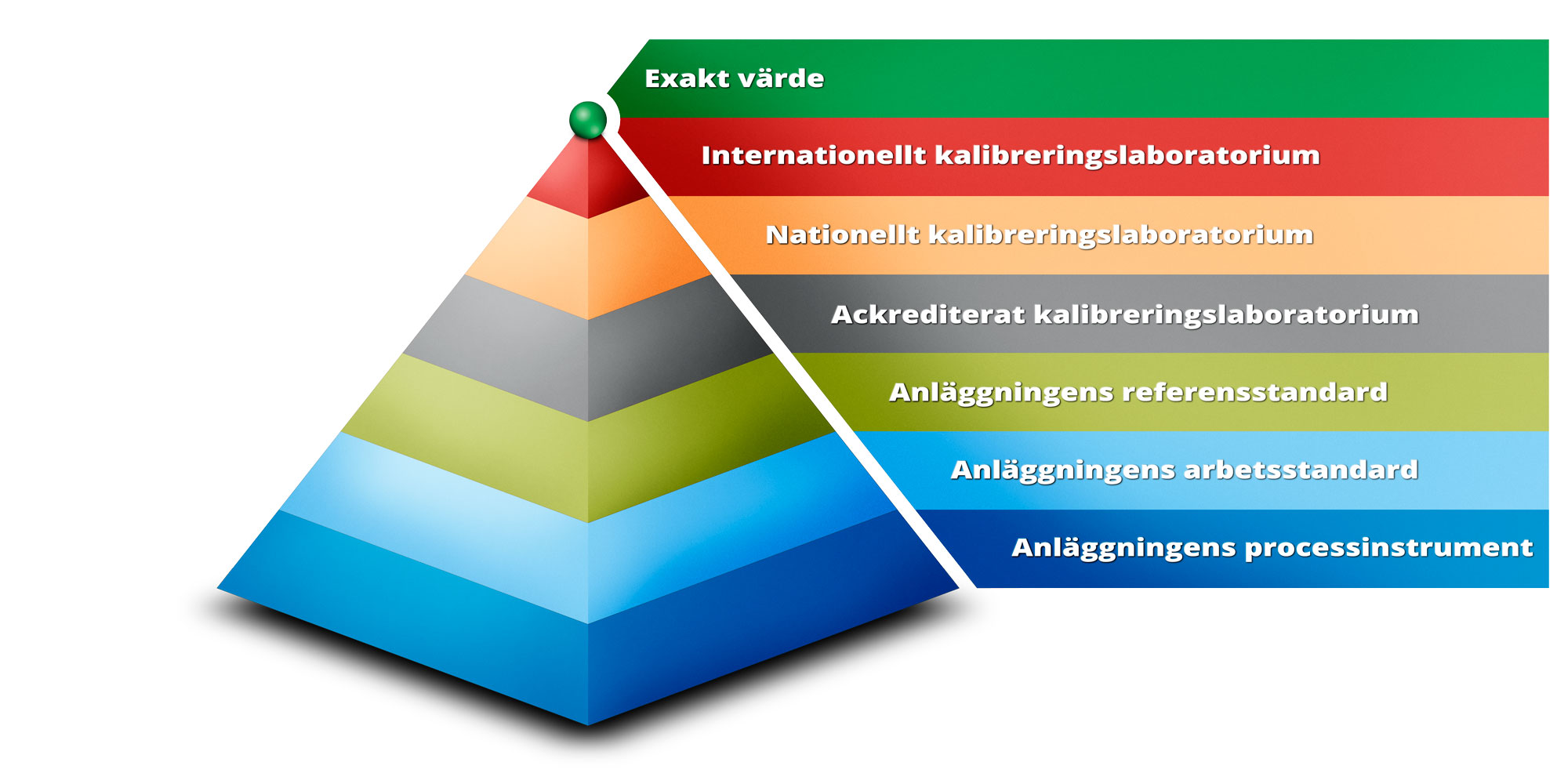
Din referensnormal (kalibrator) och dess spårbarhet 

Ofta är en av de största källorna till mätosäkerhet den referensnormal (eller kalibrator) som du använder i dina mätningar/kalibreringar. Till att börja med bör du naturligtvis välja en lämplig referensnormal för varje mätning. Det är också viktigt att komma ihåg att det inte räcker med att använda tillverkarens noggrannhetsspecifikation som referensnormal och fortsätta använda den som mätosäkerhet för referensnormalerna i åratal. I stället måste du låta kalibrera dina referensnormaler regelbundet i ett kalibreringslaboratorium som har tillräckliga möjligheter (tillräckligt liten mätosäkerhet) att kalibrera normalen och göra den spårbar. Ge akt på den totala mätosäkerheten i kalibreringen som laboratoriet dokumenterade för din referensnormal.

Du bör också kontrollera stabiliteten hos dina referensnormaler mellan de vanliga kalibreringarna. Efter en tid har du lärt dig den verkliga mätosäkerheten hos din referensnormal och du kan använda den informationen som mätosäkerheten för din referensnormal när du kalibrerar.

Andra källor till mätosäkerhet

I föregående avsnitt rekommenderade jag att du upprepar mätningen flera gånger. Men hur är det om du ber några av dina kollegor att upprepa samma mätning? Får ni alla exakt samma resultat? Ofta finns det vissa skillnader mellan olika personer som gör mätningarna. Betyder det alltså att den som gör mätningen också påverkar mätosäkerheten? - Ja, det gör det. Detta blir fallet särskilt om instruktionerna inte är tillräckligt specifika.

Vad händer om du gör samma test, men den här gången använder du olika typer av referensnormaler (kalibratorer) för att göra mätningen? Återigen kommer du troligen att hitta skillnader. Och om referensnormalernas noggrannhet (mätosäkerhet) ligger på olika nivåer, kan du till och med få relativt stora skillnader. Inte sällan kan referensnormalen (eller kalibratorn) som används för mätningen vara en av de största källorna till mätosäkerhet!

Olika miljöförhållanden kan innebära ytterligare mätosäkerhet i vissa kalibreringar.

Om du behöver läsa av någon form av analog display (analog mätare, temperaturmätare) är läsbarheten begränsad, dvs. du kan bara läsa av den med en viss noggrannhet och det finns en risk att du läser av den felaktigt (fel betraktningsvinkel) vilket skapar mätosäkerhet. Vid digitala avläsningar är upplösningen (antal decimaler) alltid begränsad, vilket orsakar mätosäkerhet (du kan bara läsa till sista decimalen).

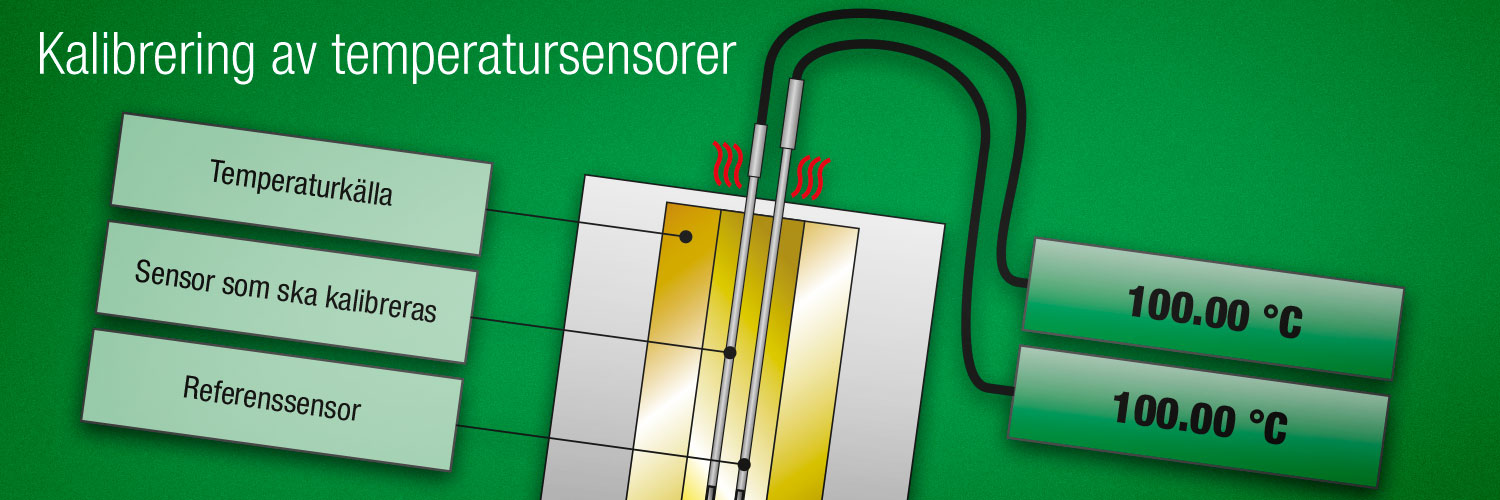
Det finns olika tekniska aspekter i kalibreringsprocessen, tillämpningar och storheter som skapar ytterligare mätosäkerheter. Till exempel vid temperaturkalibrering är det absolut nödvändigt att vänta tillräckligt länge för att temperaturen ska stabiliseras och att säkerställa korrekt nedsänkning av sonden i temperaturblocket. Vid flödeskalibrering måste du säkerställa ett stabilt flöde och vid tryckkalibrering måste man undvika eventuella läckor och ha ett stabilt tryck osv. Generellt kommer alla fluktuationer eller förändringar i den variabel som ska mätas att orsaka ytterligare mätosäkerhet.

Det finns också några slumpmässiga variabler som ger anrättningen lite extra kryddor.

Du kan också använda den experimentella standardavvikelsen som nämndes tidigare som en mätosäkerhetskomponent.

Vi kan således kort sammanfatta dessa extra källor till mätosäkerhet:

• Enhet som testas
• Referensnormal (kalibrator)
• Metod/process för att göra mätningarna/kalibreringarna
• Miljöförhållanden
• Den eller de personer som gör mätningarna
• Ytterligare mätosäkerhetskomponenter beroende på den mängd som mäts/kalibreras

Mätosäkerhetskomponenterna som listats ovan kallas mätosäkerhet av Typ B.

Att summera mätosäkerheter => sammanlagd mätosäkerhet

Typ A (standardavvikelse) är något man kan beräkna, men ofta behöver man uppskatta en del av de olika Typ B-mätosäkerheterna. När standardavvikelsen väl har beräknats och de olika mätosäkerheterna av Typ B uppskattats, är det dags att summera dem. Innan du gör det, måste du se till att alla mätosäkerheter är i samma storhet/enhet. Mätosäkerheterna bör också ha samma täckningsfaktor/konfidensnivå.

När du lägger samman mätosäkerhetskomponenter som är oberoende av varandra, räkna inte bara ihop dem, det skulle bli ett alltför pessimistiskt (värsta tänkbart) resultat. Lägg i stället ihop komponenterna med hjälp av metoden där man tar roten ur summan av kvadraterna. Med andra ord, kvadrera varje komponent, addera ihop dem sedan och ta slutligen kvadratroten ur den totala summan. Även om jag sa att det inte skulle bli några formler, kanske det ändå är lättare att förstå detta med hjälp av en relativt enkel formel:

Total mätosäkerhet =

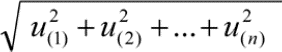
Där varje "u" är en oberoende mätosäkerhetskomponent.

Täckningsfaktor/konfidensnivå

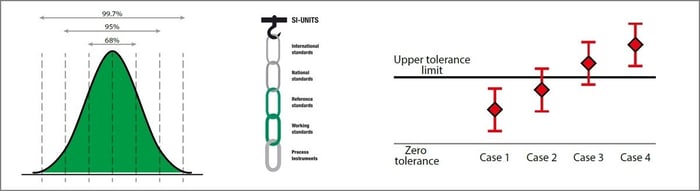
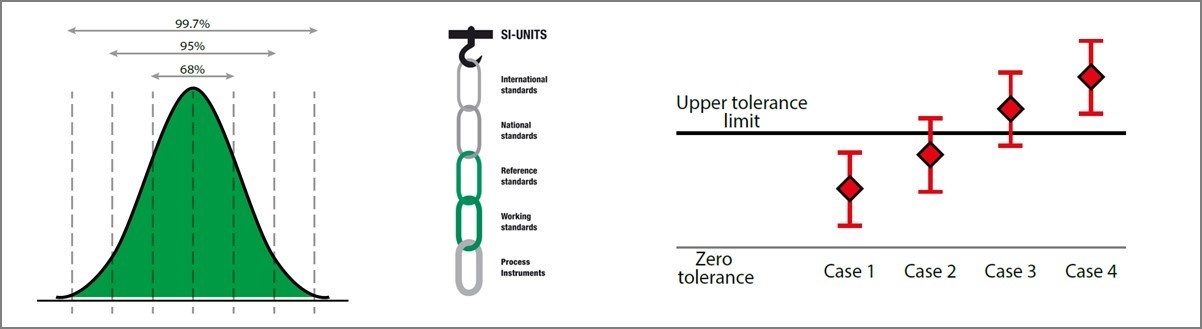
När man fastställer mätosäkerhet multipliceras den vanligtvis med en täckningsfaktor (k). Oftast multipliceras den sammanlagda mätosäkerheten med 2 (k=2 eller 2 sigma). Denna multiplikation görs för att resultatet ska få en högre konfidensnivå. När en täckningsfaktor på 2 används är den lika med en konfidensnivå på 95 %. Det här görs eftersom vi har att göra med statistiska data och enligt normal (gaussisk) fördelning ligger 95 % av resultaten inom 2 sigmaintervallet. I praktiken innebär detta att om vi använder 2 sigma, kommer 95 % av resultaten att ligga inom den givna osäkerhetsbudgeten. Olika sigmavärden ger följande konfidensnivåer:

• 1 sigma (k=1) = 68 % konfidensnivå (68 % av resultaten är inom)
• 2 sigma (k=2) = 95 % konfidensnivå
• 3 sigma (k=3) = 99,7 % konfidensnivå

Normal (gaussisk) fördelning

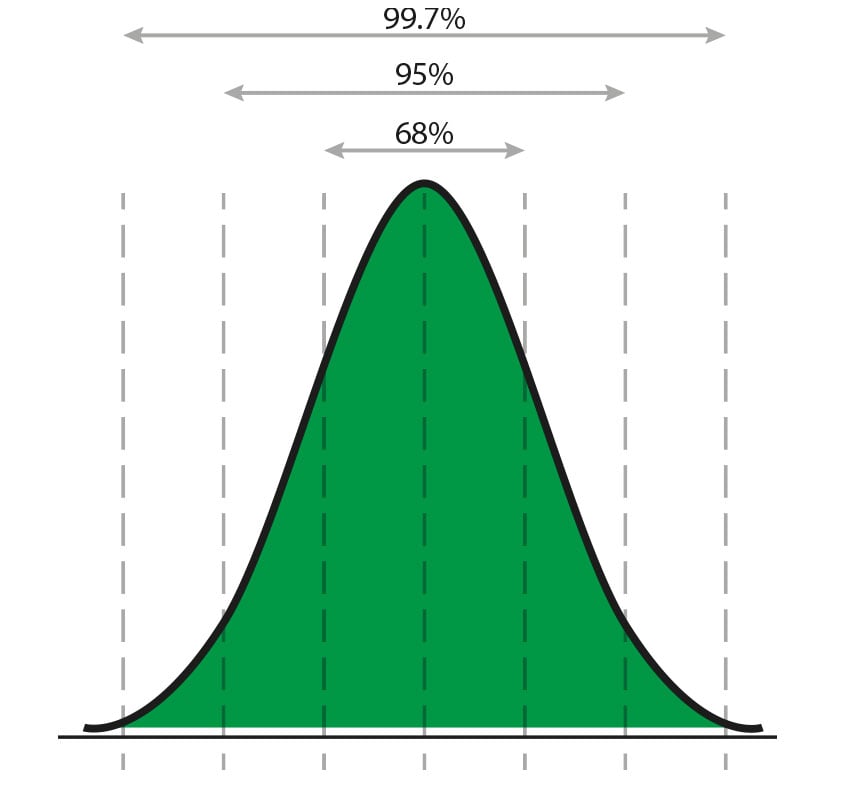
När du adderar ihop olika mätosäkerhetskomponenter, se till att de alla har samma 1 sigmavärden innan du lägger ihop dem.

Utvidgad mätosäkerhet

Innan den kombinerade mätosäkerhetskomponenten publiceras, måste du multiplicera resultatet med det valda sigmavärdet för att få den konfidensnivå som krävs. Det du får efter att ha gjort multiplikationen kallas för utvidgad mätosäkerhet, dvs mätosäkerhet som inkluderar en viss konfidensnivå.

Så här anger du mätosäkerhet i resultat och kalibreringscertifikat

I dina kalibreringsresultat bör du ange mätosäkerheten som ± värde och även nämna täckningsfaktorn/konfidensnivån. Till exempel kan du säga att temperaturen är: 20,5 °C med en mätosäkerhet på ±0,1 °C (k=2).

Försäkran om regelefterlevnad – godkänt eller underkänt

Oftast innehåller kalibreringen av ett instrument ett acceptanskriterium, dvs toleransgränser. När resultatet ligger inom gränserna anses det vara godkänt och ligger det utanför anses det vara underkänt. Det finns olika tolkningar om/hur mätosäkerheten ska beaktas när man besluter om resultatet är Godkänt/Underkänt.

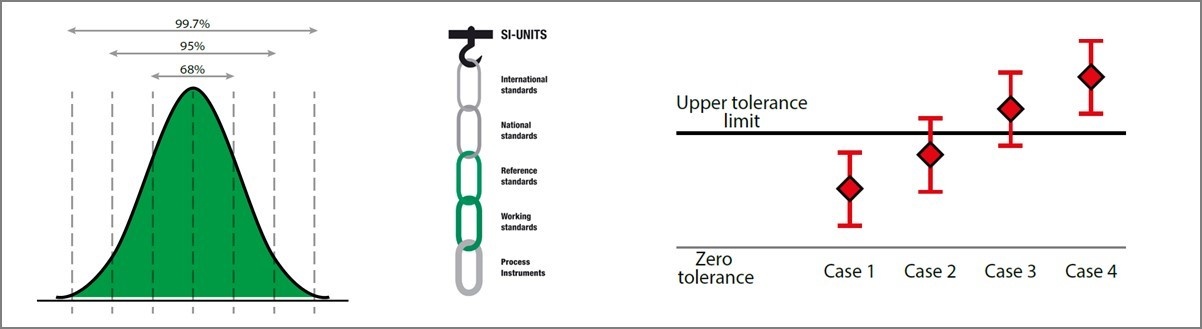
Låt oss ta några exempel för att studera olika fall. På bilden nedan illustrerar diamantfiguren mätresultatet och linjen ovanför och under anger den totala mätosäkerheten för mätningen.

Vi kan tolka de olika fallen här ovan som följande:

• Fall 1: Här ligger resultatet ganska klart inom toleransgränserna, även när mätosäkerheten beaktas. Så det här resultatet kan vi konstatera vara väl "Godkänt".
• Fall 4: Det här är också ett ganska klart fall. Resultatet ligger utanför toleransgränserna, även när mätosäkerheten beaktas. Så det här resultatet kan vi säga är dåligt, med andra ord "Underkänt".
• Fall 2 och Fall 3: Dessa fall är lite svårare att bedöma. Visst, i fall 2 verkar resultatet ligga inom toleransen medan det i fall 3 är utanför, speciellt om man inte bryr sig om mätosäkerheten. Men om vi tar mätosäkerheten i beaktande kan vi inte konstatera det med full konfidens dvs. säkerhet.

Det finns bestämmelser (till exempel; ILAC G8:1996 - Guidelines on Assessment and Reporting of Compliance with Specification; EURACHEM / CITAC Guide: Use of uncertainty information in compliance assessment, First Edition 2007) för hur man anger att kalibreringen överensstämmer med regelverket. I de här riktlinjerna föreslås att ett resultat anges som godkänt endast när felet adderat med mätosäkerheten är mindre än toleransgränsen. I riktlinjerna föreslås också att resultatet ska anges som underkänt endast när felet adderat med mätosäkerheten (eller subtraherat) är större än toleransgränsen. När resultatet ligger närmare toleransgränsen än halva mätosäkerheten föreslås det att man kallar det för en ”odefinierad” situation, dvs. man ska varken ange det som godkänt eller underkänt.

Vi har sett många människor tolka mätosäkerheten och beslut om godkänt/underkänt resultat på många olika sätt genom åren. I praktiken beaktas mätosäkerheten oftast inte vid beslutet om godkänt/underkänt, men det är ändå väldigt viktigt att vara medveten om mätosäkerheten, när man fattar beslutet.

Exempel på mätosäkerhet

Figuren nedan visar några exempel på vad olika mätosäkerheter kan innebära i praktiken.

Fall 1 och 2 har samma mätresultat, så utan mätosäkerhet skulle vi betrakta dessa som likvärdiga mätningar. Men när man tar mätosäkerheten i beaktande kan vi se att fall 1 verkligen är förfärligt eftersom mätosäkerheten helt enkelt är för stor för att kunna användas för denna mätning med de givna toleransgränserna.

När man tittar på fall 3 och 4 verkar det som att fall 3 är bättre, men när man beaktar mätosäkerheten ser vi att det inte är tillräckligt bra för att få godkänt, medan fall 4 är det.

Återigen vill jag lyfta fram att vi måste känna till mätosäkerheten innan vi kan bedöma ett mätresultat. Utan mätosäkerhetsberäkningen ser ovanstående fall 1 och 2 likadana ut, trots att de är mycket olika om man tar mätosäkerheten i beaktande.

Ett exempel från verkliga livet

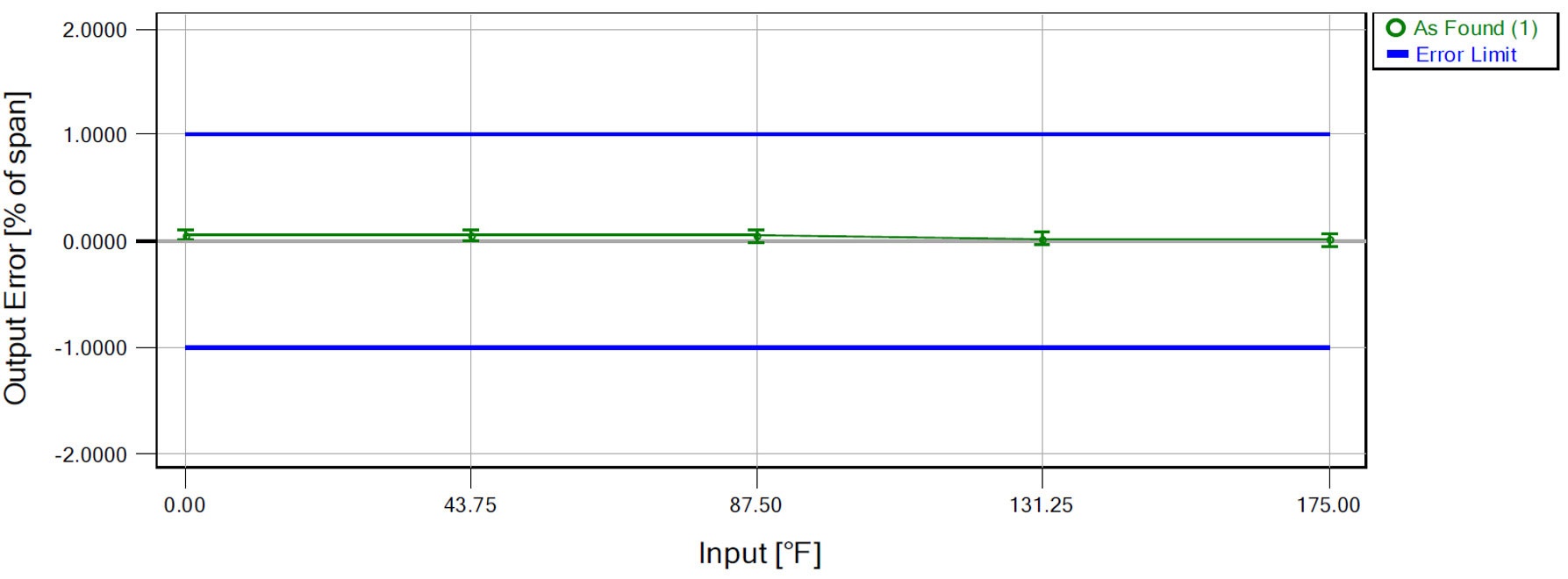
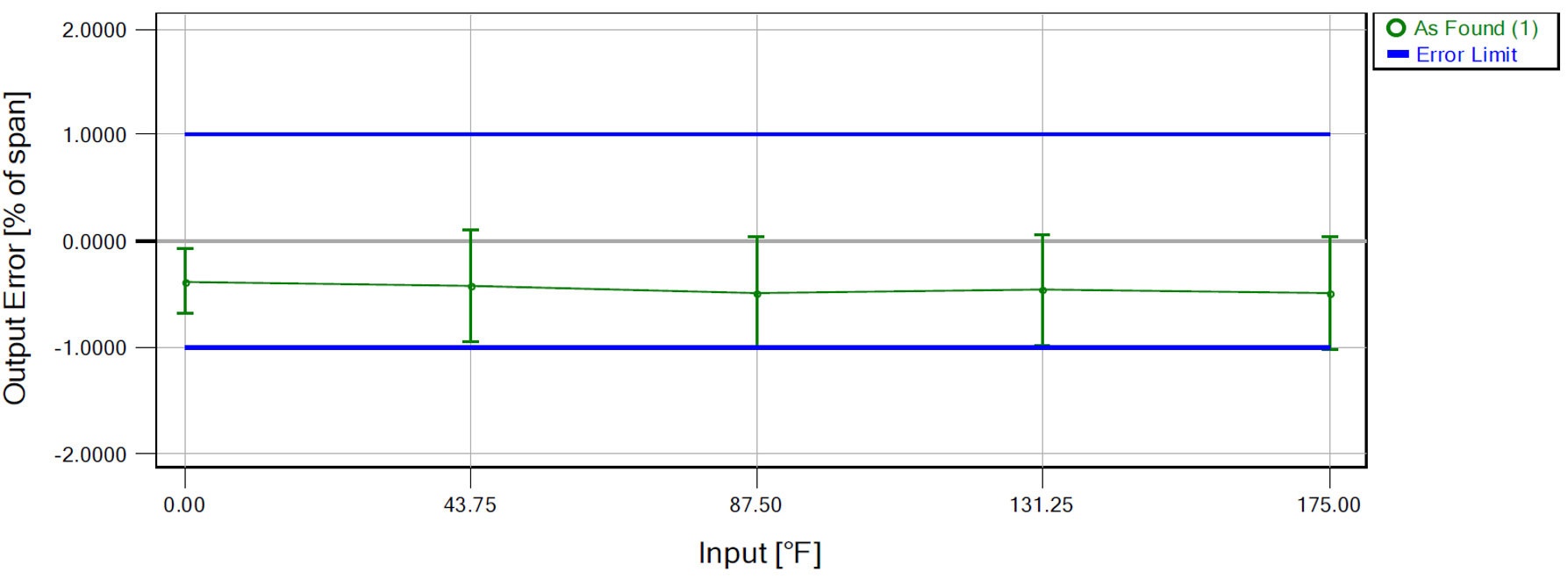
Nedan finns ett exempel från verkliga livet där samma RTD-temperaturgivare har kalibrerats med två olika kalibratorer. Grafiken skapades med Beamex CMX kalibreringsmjukvara. I det första fallet är det uppenbart att resultatet är mycket bra och även den gröna vertikala mätosäkerhetslinjen är väldigt kort, vilket indikerar att mätosäkerheten är mycket liten. I det andra fallet kan du se att resultatet är lite sämre, men mätosäkerheten för den kalibratorn är mycket sämre.

Tja, det behöver väl inte framhållas att det första fallet gjordes med en kalibrator från Beamex... ;-)

Hur som helst, när man ser mätosäkerheten framställd grafiskt är det inte svårt att förstå hur viktig den är.

TUR/TAR-förhållande kontra mätosäkerhetsberäkning

TUR (test uncertainty ratio, ung. testosäkerhetsförhållande), eller TAR (test accuracy ratio, ung. testnoggrannhetsförhållande) nämns ofta i olika publikationer. I korthet betyder begreppen att om du vill kalibrera ett 1 % instrument och du vill ha förhållandet 4:1, bör din testutrustning vara 4 gånger mer exakt, dvs. ha en noggrannhet på 0,25 % eller bättre. Vissa publikationer antyder att om man har ett tillräckligt stort TUR/TAR-förhållande behöver man inte oroa sig för någon mätosäkerhetsuppskattning/-beräkning. Det är rätt vanligt att förhållandet 4:1 används och vissa guider/publikationer rekommenderar också det förhållandet.

Oftast används förhållandet som i exemplet ovan, dvs. bara för att jämföra specifikationerna för DUT (Device Under Test, enheten som testas) med tillverkarens specifikationer för referensnormalen. Men i det scenariot tar du bara hänsyn till specifikationerna för referensnormalen (testutrustning, kalibrator) och du bortser från alla andra relaterade mätosäkerheter. Även om detta kan vara "tillräckligt bra" för vissa kalibreringar, beaktar det här systemet inte några av de största källorna till mätosäkerhet. Så det rekommenderas verkligen att man utvärderar/beräknar mätosäkerheten för hela kalibreringsprocessen.

Vi får också ganska ofta frågan: "Hur många gånger mer noggrann bör kalibratorn vara jämfört med enheten som ska kalibreras?" Även om det skulle gå att ge några förslag, så finns det inte riktigt något korrekt svar på den frågan. I stället bör du vara medveten om den totala mätosäkerheten i dina kalibreringar, vilket självklart bör återspegla dina behov!

Några användbara resurser i ämnet

• EA-4/02 - Evaluation of the Uncertainty of Measurement in Calibration (Utvärdering av mätosäkerhet vid kalibrering)
• ILAC G8:1996 - Guidelines on Assessment and Reporting of Compliance with Specification (Riktlinjer för bedömning och rapportering av specifikationsefterlevnad)
• EURACHEM / CITAC Guide: Use of uncertainty information in compliance assessment, First Edition 2007 (Användning av osäkerhetsinformation vid efterlevnadsbedömning, första upplagan 2007)
• ISO/IEC 17025:2005 - Allmänna kompetenskrav för provnings- och kalibreringslaboratorier (SIS)
• ISO 9001:2015 - Ledningssystem för kvalitet -- Krav (SIS)
• ISO 10012:2003 - Ledningssystem för mätning -- Krav på mätprocesser och mätutrustning (SIS)
• JCGM 101:2008 - Evaluation of measurement data — Guide to the expression of uncertainty in measurement (Utvärdering av mätdata — Guide för hur man anger mätosäkerhet vid mätning)

Sammanfattning

Jag hoppas att den här bloggen har gett dig litet praktisk förståelse för ämnet mätosäkerhet.

Låt mig mycket kort sammanfatta de viktigaste aspekterna av några av huvudämnena:

• Se till att skilja mellan "fel" och "mätosäkerhet"
• Experimentera genom att göra flera repetitioner av mätningarna för att få fram den typiska avvikelsen
• Använd lämpliga referensnormaler (kalibratorer) och se till att de har en giltig spårbarhet till nationella standarder och att mätosäkerheten i kalibreringen är känd och lämpar sig för dina tillämpningar
• Fundera på om effekten av miljöförhållandena har en betydande inverkan på mätosäkerheten i dina mätningar
• Var medveten om läsbarheten och bildskärmsupplösningen för olika indikeringsanordningar
• Studera de specifika viktiga faktorerna för de storheter du kalibrerar
• Bekanta dig med metoden där man tar "roten ur summan av kvadraterna" för att summera oberoende mätosäkerheter
• Var medveten om täckningsfaktorn/konfidensnivån/den utvidgade mätosäkerheten gällande mätosäkerhetskomponenterna
• I stället för, eller i tillägg till TUR/TAR-förhållandet, sträva efter att vara mer medveten om alla relaterade mätosäkerheter
• Var uppmärksam på den totala mätosäkerheten i kalibreringsprocessen innan du beslutar om ett resultat är godkänt/underkänt.
• Om du har kommentarer eller frågor, och det hoppas jag att du har, vill vi gärna att du hör av dig! Kontakta oss på www.beamex.com eller beamex.se@beamex.com

Ladda ner artikeln gratis

Ladda ner artikeln gratis som PDF genom att klicka på bilden nedan: